(Source-simplilearn.com)
In the world of data analysis and machine learning, hierarchical clustering is a really important technique that helps us understand how different pieces of data are related to each other. This article is here to explain hierarchical clustering in a way that’s easy to understand, breaking down its main ideas, how it’s used, and the benefits it brings.
What is Hierarchical Clustering?
Hierarchical clustering, also known as hierarchical cluster analysis or HCA, is a method of cluster analysis that seeks to build a hierarchy of clusters. It groups similar data points into clusters and then repeatedly merges them based on similarity until a single cluster encompassing all data points is formed.
How Does Hierarchical Clustering Work?
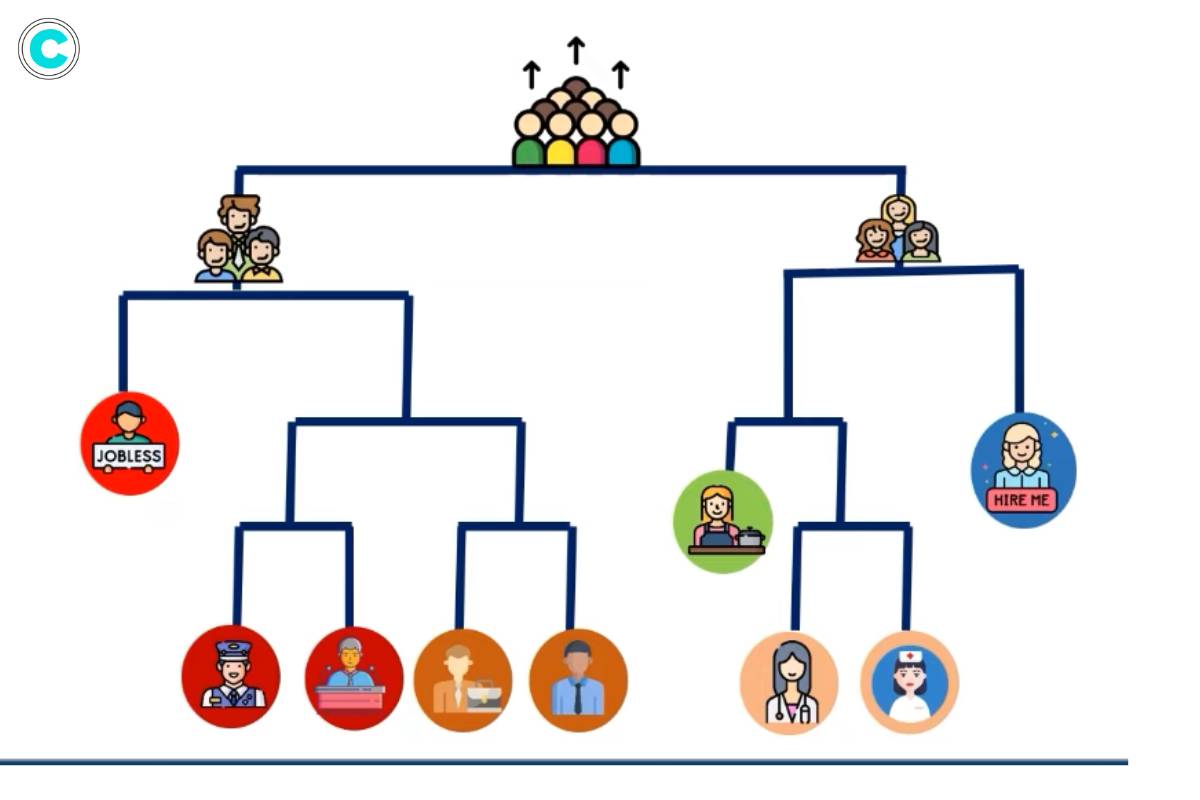
Hierarchical clustering is a method of cluster analysis that seeks to build a hierarchy of clusters. It can be approached in two ways: agglomerative and divisive.
1. Agglomerative Clustering
Agglomerative clustering, also known as the bottom-up approach, starts with each data point as a separate cluster and then merges the closest pairs of clusters until only one cluster remains. This process is performed iteratively, with clusters being merged based on their similarity or proximity. The merging of clusters continues until all data points belong to a single cluster. The results of agglomerative clustering are usually presented in a dendrogram, which is a tree-like structure that shows the hierarchical relationships between clusters.
2. Divisive Clustering
Divisive clustering, also known as the top-down approach, takes the opposite approach. It begins with all data points in one cluster and then divides them recursively into smaller clusters based on dissimilarity. This process continues until each data point becomes a separate cluster. Divisive clustering is more complex compared to agglomerative clustering, as it requires a flat clustering method as a subroutine.
Both agglomerative and divisive clustering can use various distance metrics and linkage methods to determine the similarity or dissimilarity between clusters. Some commonly used linkage methods include single linkage, complete linkage, average linkage, and Ward’s method.
Hierarchical clustering has the advantage that any valid measure of distance can be used, making it a flexible and versatile clustering technique. It is commonly used in various fields, such as image processing, information retrieval, and data mining.
Applications of Hierarchical Clustering

Hierarchical clustering finds applications across various domains due to its flexibility and ability to reveal the hierarchical structure of data. Here are some examples:
1. Biology: It is widely used in biological taxonomy to classify organisms based on their evolutionary relationships. It helps in grouping animals or species according to their biological features to reconstruct phylogeny trees.
2. Customer Segmentation: Businesses employ it to segment customers based on their purchasing behaviors. By grouping customers into clusters, businesses can develop targeted marketing strategies and personalize their approach to different customer segments.
3. Image Analysis: In image processing, it helps in segmenting images into meaningful regions based on pixel intensities or colors. It aids in image segmentation, object recognition, and computer vision tasks.
4. Document Clustering: Text documents can be clustered hierarchically to organize and retrieve information efficiently. It can group similar documents together, making it easier to navigate and search through large collections of documents.
5. Anomaly Detection: It can be used for anomaly detection in datasets. By isolating data points that do not fit well within any cluster, it can identify outliers or anomalies in the data. This is useful in various domains, such as fraud detection, network intrusion detection, and outlier detection in sensor data.
These are just a few examples of the applications of hierarchical clustering. It is a versatile technique that can be applied in various fields where grouping or organizing data based on similarity is required.
Advantages of Hierarchical Clustering

Hierarchical clustering offers several advantages that make it a popular choice in various applications. Here are some key advantages:
1. Interpretability:
The hierarchical structure of clusters provides a clear visualization of the relationships between data points. The dendrogram representation allows for easy interpretation of the nested structure of the clustering, making it easier to understand and analyze the results.
2. No Need for Prior Information:
Unlike some clustering algorithms, it does not require prior knowledge about the number of clusters in the data. It can automatically determine the number of clusters based on the data and the chosen linkage method.
3. Flexibility:
It allows for the exploration of different levels of granularity in clustering. It provides insights into both global and local structures within the data. By examining different levels of the dendrogram, users can gain a deeper understanding of the data and identify meaningful subclusters.
4. Hierarchical Representation:
The hierarchical dendrogram representation of clusters allows for the identification of subclusters and their relationships. This aids in insightful analysis and can provide valuable insights into the structure of the data.
5. Robustness:
It is robust to noise and outliers since it does not rely on a single distance metric or initialization. It considers the overall structure of the data and can handle noisy or incomplete data effectively.
These advantages make hierarchical clustering a valuable tool in various domains, including biology, customer segmentation, image analysis, document clustering, and anomaly detection.
FAQs
1. Can hierarchical clustering handle large datasets?
Hierarchical clustering can be computationally intensive for large datasets due to its quadratic time complexity. However, there are techniques such as hierarchical clustering with optimized algorithms and approximate methods that can handle large datasets more efficiently.
2. How do I choose the appropriate distance metric for hierarchical clustering?
The choice of distance metric depends on the nature of your data and the underlying relationships you want to capture. Common distance metrics include Euclidean distance, Manhattan distance, and cosine similarity, among others.
3. Is hierarchical clustering sensitive to outliers?
Hierarchical clustering can be sensitive to outliers, especially in agglomerative methods where outliers can influence the merging process. Preprocessing techniques such as outlier removal or robust distance metrics can mitigate this sensitivity.
4. Can hierarchical clustering handle non-numeric data?
Yes, hierarchical clustering can handle non-numeric data by using appropriate distance measures or similarity functions tailored to the data type, such as Jaccard distance for binary data or edit distance for textual data.
5. How do I interpret a dendrogram produced by hierarchical clustering?
A dendrogram visually represents the clustering hierarchy, with each branch representing a cluster merge and the height indicating the dissimilarity between clusters. The horizontal axis represents the individual data points or clusters, and the vertical axis represents the distance or dissimilarity. Clusters are formed by cutting the dendrogram at a desired height or distance threshold.

A Guide to Master Machine Learning Pattern Recognition:
At its core, machine learning pattern recognition involves the process of training algorithms to identify and interpret patterns within datasets, enabling them to make predictions, classifications, or
In conclusion, hierarchical clustering is a versatile and powerful technique for exploring the structure of data and uncovering hidden patterns. By understanding its principles and applications, analysts and data scientists can harness its potential to gain valuable insights from complex datasets.






