^{(Source – Medium)}

Linear models are really important when it comes to statistical analysis and machine learning. They’re like the building blocks that help us understand and predict how different things are related to each other. Whether you’re a data scientist, a statistician, or just someone who loves looking at data, it’s super important to understand these models. In this article, we’ll dive into the key things you need to know about them, how they’re used in different fields, and why they’re so crucial. 

What Are Linear Models?

These are mathematical equations that describe the relationship between two or more variables using a linear equation. They are widely used in various fields, including statistics, economics, and machine learning, to analyze and predict relationships between variables.

The most basic form of a linear model is the simple linear regression model, which involves one dependent variable and one independent variable. The relationship between the dependent variable (Y) and the independent variable (X) is represented by a linear equation:

Y = β0 + β1X + ϵ

In this equation:

• Y represents the dependent variable.
• X represents the independent variable.
• β0 is the y-intercept, which represents the value of Y when X is zero.
• β1 is the slope of the line, which represents the change in Y for a one-unit change in X.
• ϵ represents the error term, which accounts for the variability in Y that is not explained by the linear relationship with X.

These can also include multiple independent variables, resulting in multiple linear regression models. The equation expands to include the additional independent variables:

Y = β0 + β1X1 + β2X2 + … + βnXn + ϵ

In this case, X1, X2, …, Xn represent the multiple independent variables, and β1, β2, …, βn represent their respective slopes.

These can be used for various purposes, such as predicting the value of the dependent variable based on the independent variables, assessing the strength of the relationship between variables, and identifying the significance of the independent variables in explaining the variation in the dependent variable.

Types of Linear Models

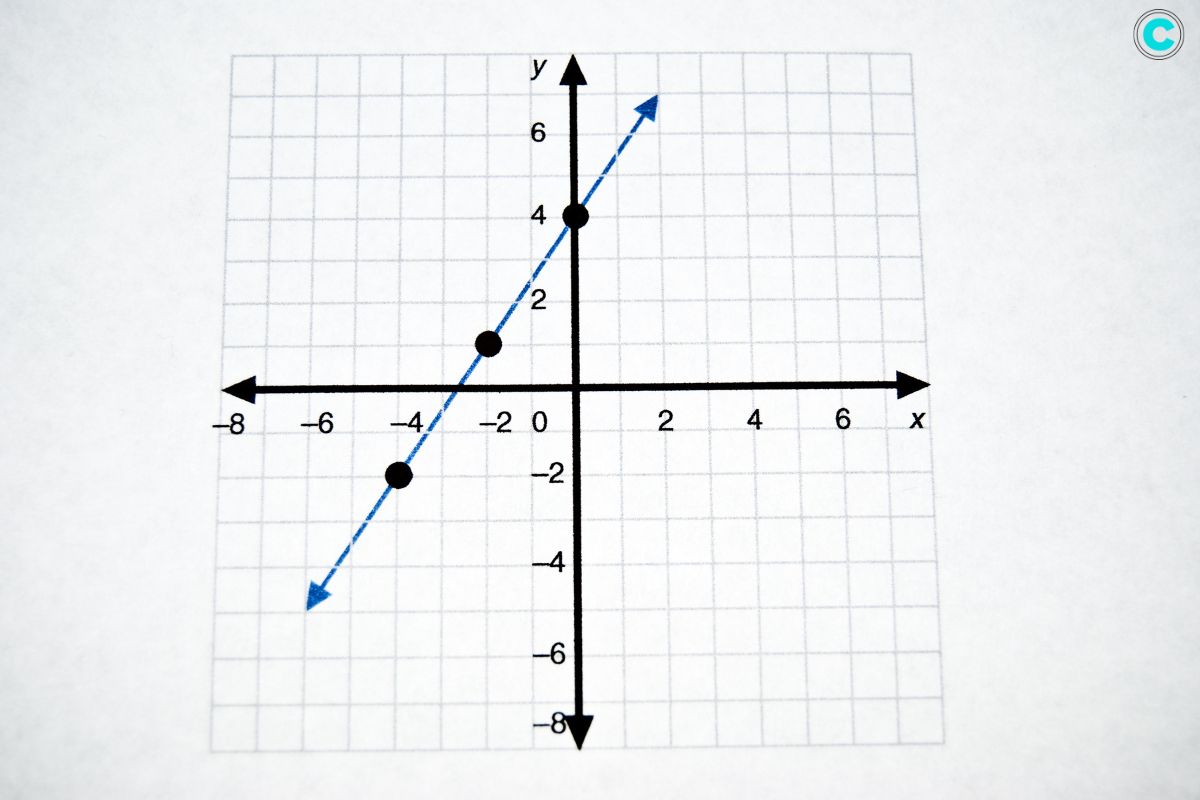
1. Simple Linear Regression: This type of linear model involves one independent variable and one dependent variable. It aims to establish a linear relationship between the two variables.
2. Multiple Linear Regression: This model includes multiple independent variables to predict the dependent variable. It expands the simple linear regression equation to include the additional independent variables.
3. Logistic Regression: Although primarily used for classification problems, logistic regression can be considered a type of linear model where the dependent variable is categorical. It estimates the probability of an event occurring based on the independent variables.
4. Ridge Regression: Ridge regression is a technique used when the data suffers from multicollinearity, which is the high correlation between independent variables. It adds a penalty term to the linear equation to reduce overfitting.
5. Lasso Regression: Similar to ridge regression, lasso regression also adds a penalty term but tends to produce simpler models by shrinking some coefficients to zero. This effectively performs variable selection, as it identifies the most important independent variables.

Applications of Linear Models

These are versatile and have a wide range of applications:

1. Predictive Analytics: Used extensively in predictive analytics, these help forecast trends and make predictions based on historical data.
2. Economics: Economists use these models to understand and predict economic activities, such as consumer spending and investment behaviors.
3. Healthcare: In healthcare, these models help in predicting patient outcomes based on various factors like age, weight, and medical history.
4. Marketing: Marketers use these models to predict customer behavior, such as purchasing patterns and responses to marketing campaigns.
5. Engineering: Engineers apply these models in control systems, signal processing, and reliability analysis.

Advantages of Linear Models

1. Simplicity: These are relatively easy to understand and interpret. They provide a straightforward way to assess relationships between variables.
2. Efficiency: These models are computationally efficient and can handle large datasets with ease.
3. Flexibility: Despite their simplicity, these models can be extended and adapted to fit more complex data structures.
4. Good Baseline: these models serve as a good baseline for comparison with more complex models.

Limitations of Linear Models

1. Linearity Assumption: These models assume a straight-line relationship between the independent and dependent variables, which might not always be the case.
2. Sensitivity to Outliers: These models can be heavily influenced by outliers, which can skew the results.
3. Overfitting and Underfitting: Simple linear models might underfit complex data, while adding too many variables in multiple linear regression might lead to overfitting.
4. Multicollinearity: In multiple linear regression, high correlation among independent variables can make it difficult to assess the individual effect of each variable.

How to Build Linear Models

Building a linear model involves several steps:

1. Data Collection: Gather data relevant to the problem you are trying to solve.
2. Data Cleaning: Clean the data to handle missing values, outliers, and inconsistencies.
3. Exploratory Data Analysis (EDA): Analyze the data to understand the relationships between variables.
4. Model Selection: Choose the appropriate type of linear model based on your data and the problem.
5. Model Training: Use a portion of your data to train the model, fitting the linear equation to the data points.
6. Model Evaluation: Evaluate the model’s performance using metrics such as R-squared, Mean Squared Error (MSE), and Root Mean Squared Error (RMSE).
7. Model Tuning: Fine-tune the model to improve its performance by adjusting parameters and potentially adding penalty terms like in ridge or lasso regression.
8. Deployment: Once satisfied with the model’s performance, deploy it for practical use in predictions or decision-making processes.

FAQs

1. What is the main difference between simple and multiple linear regression?

Simple linear regression involves one independent variable, whereas multiple linear regression involves two or more independent variables.

2. How do you handle multicollinearity in linear models?

Multicollinearity can be handled by using techniques like ridge regression, lasso regression, or by removing highly correlated predictors.

3. Why are linear models popular in predictive analytics?

These models are popular in predictive analytics due to their simplicity, efficiency, and ease of interpretation.

4. Can linear models be used for classification problems?

Yes, logistic regression is a type of linear model used for binary classification problems.

5. What are some common metrics to evaluate the performance of a linear model?

Common metrics include R-squared, Mean Squared Error (MSE), and Root Mean Squared Error (RMSE).

Your Ultimate Guide to the Top 9 Machine Learning Books in 2024

These books will help you learn the basics or level up your skills with the latest techniques and algorithms. So, get ready to enhance your understanding and

Read More:

Conclusion

Linear models are indispensable in the realm of data analysis. Their ability to provide clear and interpretable relationships between variables makes them a preferred choice for many analytical tasks. Understanding and effectively applying these models can significantly enhance decision-making processes across various domains.